Antwort Wie berechnet man Trigonometrie? Weitere Antworten – Was sind trigonometrische Berechnungen
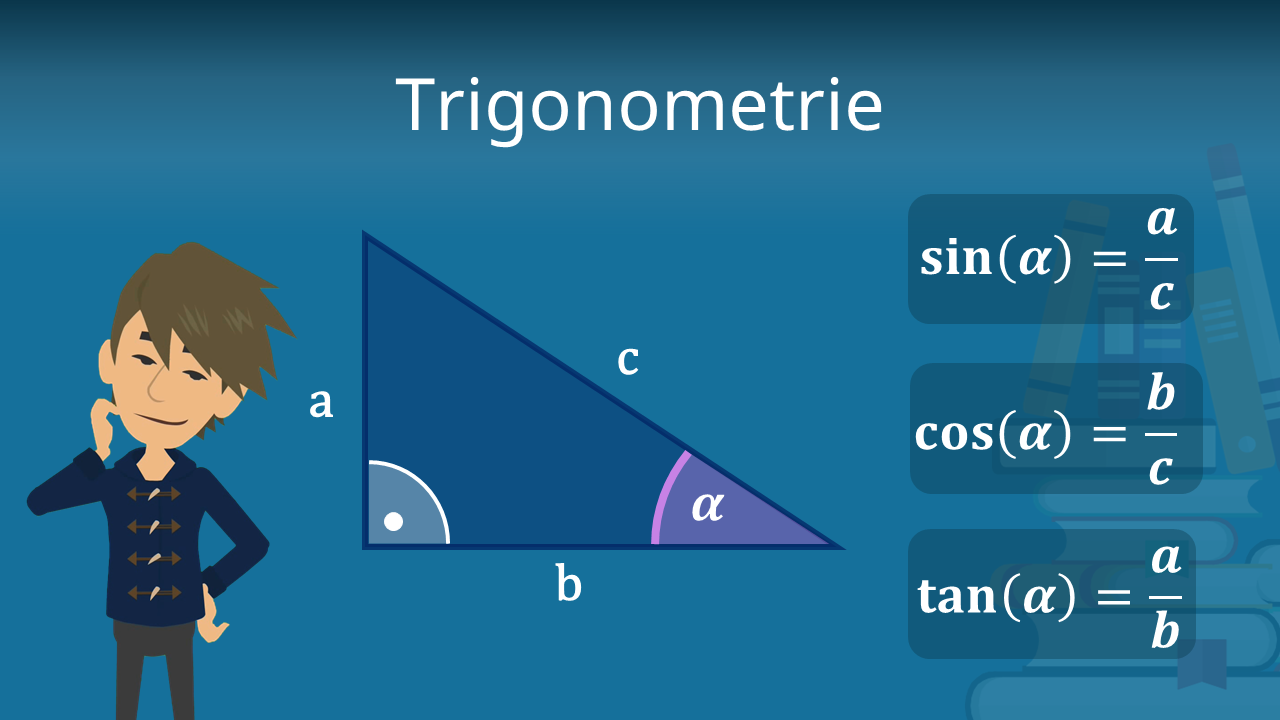
Trigonometrische Formeln – Definition
In der sogenannten Trigonometrie geht es um die Seitenverhältnisse von Dreiecken. Für die Anwendung der trigonometrischen Formeln benötigt man also Kenntnisse über die Seitenverhältnisse im rechtwinkligen Dreieck. Diese werden immer in Bezug auf einen gegebenen Winkel angegeben.Tangens: Formeln
Auf diese Formeln kommst du durch Umformung der Grundformel tan(\alpha) = \frac{Gegenkathete}{Ankathete}. Daher musst du diese Formeln nicht auswendig lernen.Sinus, Kosinus und Tangens am rechtwinkligen Dreieck
Der Sinus, Kosinus und Tangens sind Verhältnisse von Seitenlängen in einem rechtwinkligen Dreieck. Diese sind abhängig von einem der beiden spitzen Winkel des Dreiecks. Außerdem sind der Sinus, Kosinus und Tangens die drei wichtigsten trigonometrischen Funktionen.
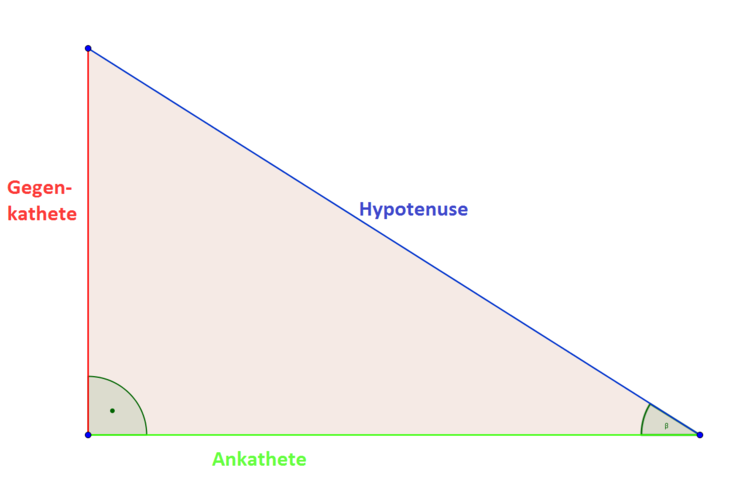
Wie schwer ist Trigonometrie : Trigonometrie kann am Anfang etwas schwer zu verstehen sein, aber nach etwas Übung wirst du sie meistern! Hier sind einige Tipps zur Trigonometrie: Beschrifte die Hypotenuse, die Ankathete und die Gegenkathete deines Dreiecks, damit du herausfinden kannst, welche Identität du verwenden musst.
Wann lernt man Trigonometrie
In der 8. Klasse Mathe der Realschule Bayern hast du gelernt Dreiecke zu zeichnen bzw. auch mit Zirkel und Lineal zu konstruieren. Längen oder Winkel wurden sodann aus der Zeichnung abgelesen, eine Berechnung ist jetzt durch diesen Bereich “Trigonometrie” möglich.
Wie berechnet man Sinus und Cosinus : sin²(α) + cos²(α) = 1
Mit Hilfe dieser Beziehung kannst du ohne Taschenrechner zu jedem Winkel den Sinus aus dem Kosinus oder den Kosinus aus dem Sinus bestimmen. Wenn sin(α)=0.6 , dann cos(α)=0.8 .
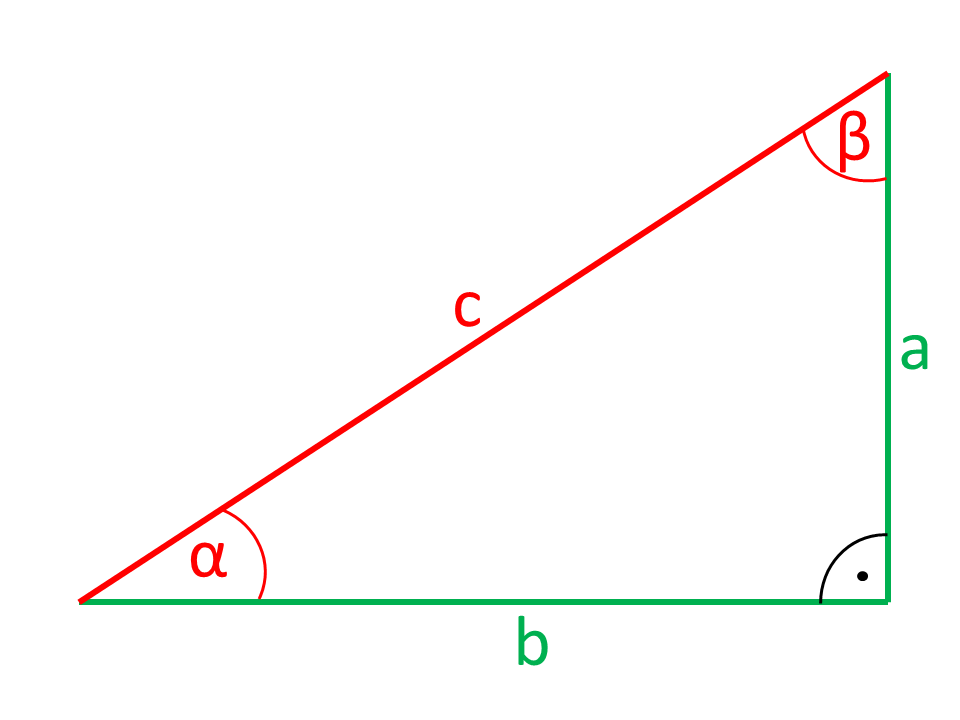
Die Winkelfunktionen Sinus, Kosinus und Tangens verwendest du, wenn du die Länge einer Seite oder die Größe eines Winkels in einem rechtwinkligen Dreieck berechnen möchtest.
sin²(α) + cos²(α) = 1
Mit Hilfe dieser Beziehung kannst du ohne Taschenrechner zu jedem Winkel den Sinus aus dem Kosinus oder den Kosinus aus dem Sinus bestimmen. Wenn sin(α)=0.6 , dann cos(α)=0.8 .
Wie lässt sich der Tangens aus Sinus und Cosinus berechnen
- sin(\alpha) = Hypotenuse / Gegenkathete.
- tan(\alpha) = Gegenkathete / Ankathete.
- cos(\alpha) = Ankathete / Hypotenuse.
Die Trigonometrie liefert Methoden, um fehlende Seitenlängen und Winkelgrößen von Dreiecken zu berechnen, wenn drei dieser Größen gegeben sind. Hier findest du viele Erklärungen und Übungen mit denen Du die wichtigen Themen in der Trigonometrie lernen kannst.Das Vorgehen ist also ähnlich wie beim Sinus, nur mit der Ankathete anstatt der Gegenkathete eines Winkels. Auf diese Formeln kommst du durch Umformung der Grundformel cos (\alpha)= \frac{Ankathete}{Hypotenuse}.
Trigonometrie – Lernvideos und Aufgaben (Mathe 10. Klasse)
Was ist der Cosinus Formel : Als allgemeine Gleichung einer Kosinusfunktion wird oft f(x)=a · cos (bx + c) + d bezeichnet. Reelle Zahlen a, b, c und d haben folgende Effekte: a streckt entlang der y-Achse.
Wann rechne ich Sinus : Sinussatz. Den Sinussatz kannst du benutzen, um fehlende Stücke eines Dreiecks zu berechnen. Zum Beispiel, wenn zwei Seitenlängen und ein gegenüber liegender Winkel oder eine Seitenlänge und zwei Winkel gegeben sind. Das Dreieck muss dabei nicht rechtwinklig sein!
Wie berechnet man die sinusfunktion
Es gibt eine allgemeine Formel für alle Nullstellen bzw. Wendestellen der Sinusfunktion: π x k = π · k . Die Ableitung der Sinusfunktion f ( x ) = sin ( x ) ist: f ' ( x ) = cos ( x ) .

Die Tangensfunktion ist periodisch, es gilt tanx=tan(x+k⋅π) (k∈Z). Der Funktionsgraph der Tangensfunktion ist punktsymmetrisch zum Ursprung, sie ist also eine sog. ungerade Funktion. Er ist außerdem auch punktsymmetrisch zu allen Nullstellen (weil die Funktion bis nach „±∞“ periodisch ist).Der Sinus, der Cosinus und der Tangens werden angewendet, um Winkel und Seiten rechtwinkliger Dreiecke zu bestimmen.
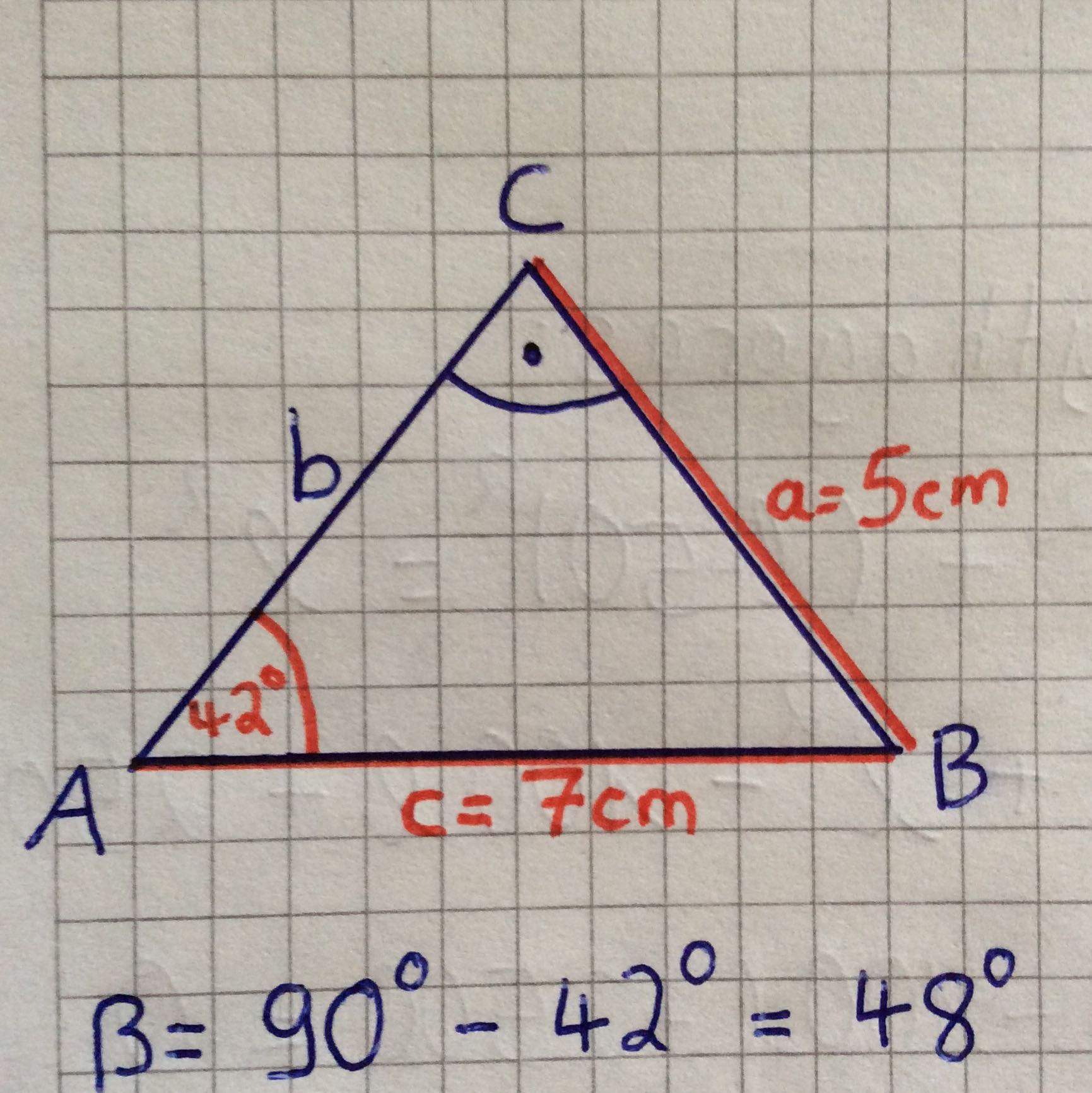
Wann wendet man Trigonometrie an : Wenn du von einem rechtwinkligen Dreieck eine Seite und einen Winkel gegeben hast, kannst du mithilfe der trigonometrischen Funktionen die restlichen Seiten berechnen.



